|
Theory |  |
Exercises |  |
 |
Lection 1: Current
In this lecture, the electric current is introduced.
Goal: The goal of this lecture is to have a basic understanding what electric current is, to know the symbols used in electric circuits to represent the current and current sources and to be able to calculate the current. This includes Kirchhoff's current law.
|
In the last chapter, the atom was introduced. You should now know, what an atom looks like, and what the different parts of an atom are.
Now the next step is the electric current. How do we go from protons, electrons and neutrons to electric current? The Answer is simple. The free moving electrons are the electric current, we are talking about. |
||
|
But how does this work? As you probably know, metals are very good conductors. Other materials will carry a current, too. But not as good as metal. That is the reason, we use metal cables for installations, such as copper or sometimes even silver and gold in small hardware pieces. In a metal, the atoms are arranged in a mesh. The large protons and neutrons, which are in the core of the atoms are too large and heavy to move, so they stay fixed where they are. But the light and small electrons are able to move around and even hop from one atom to the next. Only the electrons are able to flow. This movement of electrons is the electric current. |
||
|
How to we express how much electric charge is flowing? Well one option is to count the number of electrons and say exactly how many electrons are currently flowing through the wire per second. But, usually, there are too many electrons to count. So instead of counting these electrons exactly, we use a special unit. We count in Amperes [A]. One Ampere is as much as if 6'241'000'000'000'000'000 electrons flow through a piece of wire per second. Or to use a shorter notation:
A is the unit for ampere. So whenever we want to say how many ampere we have, we use just this letter A. 1018 means, that this is 10 * 10 * 10 * ... * 10, exactly 18 times. So for example 103 = 10 * 10 * 10 and 34 = 3 * 3 * 3 * 3. e- is the sign for one electron, that is one negative charge. s is the sign for seconds. So whenever we want to say how many seconds we have, er just use s. So we now know, that there is much negative charge in one ampere of electric current. This unit was named after monsieur Ampere who discovered the existence of electric current. You can learn more about Monsieur Ampere and the exact definition of Ampere and current here. So far we saw that current is not more than free electrons moving thourgh a piece of wire. |
|
In the next part, we will see how current is displayed in electric circuits, and how one can calculate with electric current. |
|||||
|
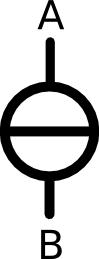
On the left is the sign for a current source.
If you want to display that an electric current is coming into your circuit, you can do this by using this symbol.
ConnectAand B to the circuit to where the current should flow into and out again. The direction of the flow is usually indicated with a little arrow. |
||||
|
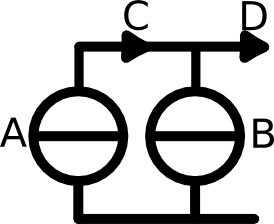
In the example to the left, we have two current sources, A and B.
The little arrow at position C shows the direction of the current coming from the current source A.
The little arrow at position D shows the direction of the current coming from both current source A and B. Now how can we add up the current coming from different current sources? At position C we have only the current coming from A. But at position D we have both the current coming from A and B. So we can simply add up the two currents. |
||||
|
Let's calculate the example from the picture above: We know, how much current is coming from the two current sources and we want to know how much current we have at position C and D. Source A: 3 A Source B: 2 A So at position C, we only have the current from A, therefore C = 3 A At position D we have the current from position C and the current from source B, so D = 3 A + 2 A = 5 A. One important last thing concerning the current sources. Current sources can not just be linked together arbitrarily. There are some rules on how to link together current sources.
We see, that all the current, that is going into a junction within a circuit, has to come out again. The charge can not just disappear. This is one of the most important laws in electric circuit, we call it Kirchhoff's Current Law (KCL). |
|||||
Kirchhoff's Current LawThis law is sometimes also called nodal law or Kirchhoff's point rule or Kirchhoff's junction rule.It just means that all the current that is flowing into a junction has to flow out again. It can not just vanish into thin air. So the total sum of all the current has to be zero, or in other words the sum of all ingoing current has to be equal to the sum of all outgoing current. |
|||||
|
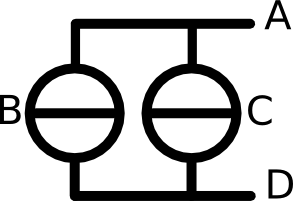
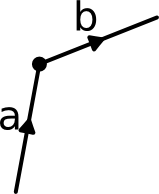
To sum up all the current, we always consider the little arrow keys to determine the direction of the current. If the arrow is pointing towards the node, then we add the current. If the arrow is pointing away from the current, then we subtract the current. See the example to the right. The sum of all current has to be zero, or in other words, all incoming current has to go out again. So the equation would be: +Ia -Ib = 0 I add the current from line a because it is flowing towards the node and I subtract the current from line b because it is flowing away from the node. Another way to formulate the Kirchhoff's law is by butting all current that flow into the node on the left side of the equation and all current flowing out of the node on the right side. So the equation would be: Ia =Ib These two equations lead to the same result. |
||||
|
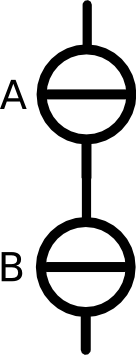
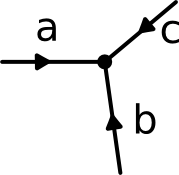
This example is a bit more complexe than the previous one. Here we have a node with three lines. According to Kirchhoff's law, the equation would be: Ia + Ic + Ic = 0 Do you see the problem? Previously, we have learned, that all current going into a node has to go out again. But here all arrows are pointing towards the node, none is pointing away from it. This means, that one of the currents has to be negative! When we draw these pictures with the arrows, we acctually do not know the true direction of the current, we just draw the arrows as we like. So It might bem that we didn't guess right. The current could acctually be flowing in the opposite direction. Then the current is negative. Let's make an examples with numbers for the picture on the left. We know that Ia = 1.25A and Ib = 3.75A The equation is then 1.25A + 3.75A + Ic = 0 This can be reformulated by using simple math: -1.25A - 3.75A = Ic so the result is: -5A = Ic |
||||
Now you know a bit about the electric current. Conclusion and short repetitonLet's briefly list all the important information from this chapter in a short list.
Now go to the exercises, to train your knowledge. The exercises are all about the first Kirchhoff's law, that you have just learned. |
|||||