Lecture 0
Lecture 1
Lecture 2
Lecture 2.1
Lecture 3
Lecture 3.1
Lecture 4
Lecture 5
Lecture 5.1
Lecture 6
Lecture 7
Lecture 8
 

Electric Circuits
in Solar Installations
Theory Exercises  

Lection 6: Electric Power

In this lecture, focus is laid on electric power


Goal: The goal of this lecture is to be able to calculate the power in an electric circuit and know the essential formula to do so.

In the last chapter, you have learned, that energy and power are two important concepts in physics. You have also seen the definition of electric power and electric energy and how they are connected. In this chapter, we will start with electric power and go into more detail on how to calculate it in a circuit.

Recall the definition of electric energy and electric power.
The unit of power is Watt [W], named after the Scottish scientist James Watt.

Note: Electric Energy and Power

NameExplanationSymbolsUnitsconnection
Energy Energy is voltage times current times time E = U * I * t [Wh] = [V] * [A] * [h] E = P * t
Power Power is voltage times current P = U * I [W] = [V] * [A] P = E / t

So far, we have had three important rules and laws:

  • Kirchhoff's nodal rule (current law)
  • Kirchhoff's loop rule (voltage law)
  • Ohm's law
The next important law you learn is the power law: P = U*I, power is voltage times current.

All electric devices need energy to run. But when you look at the detail specifications of an electric device, then it tells you how much power it needs, not how much energy. How is that so?
The energy a device needs depends on how long you want to use this device. A computer needs more energy if you use if for 5 hours than if you use it for 1 hour. So what we are actually interested is the amount of energy per time that is needed. And this is exactly the definition of power. So we want to know how much energy the computer needs per instant.

Have a look at the Raspberry Pi or some other computer that is near you. How much power does this device need? Ask a teacher if you don't know it. They might tell you its about 5 Watt. So if you want to know how much energy this device needs per hour you just multiply the power by the time: 5 Watt * 1 h = 5 Wh.

How much power does the load need?
U = 5 V
I = 2.5 A

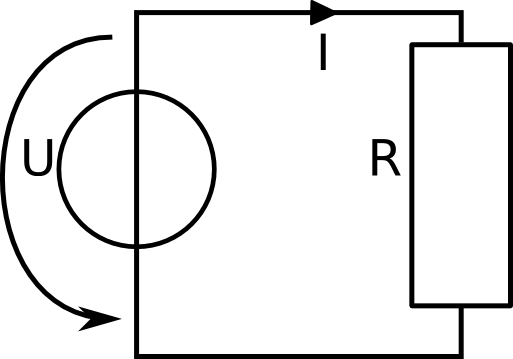
On the left, you see the simple circuit. We have measured, that the voltage source gives a voltage of 5 volt and that there is a current of 2.5 ampere in the line. We want to know how much power the device is using.
The equation to calculate this is P = U * I

P = U * I
P = 5 V * 2.5 A
P = 12.5 V*A
P = 12.5 W

This is the way we can calculate the power of a device. We multiply the voltage over that device times the curren, that is flowing through that device.

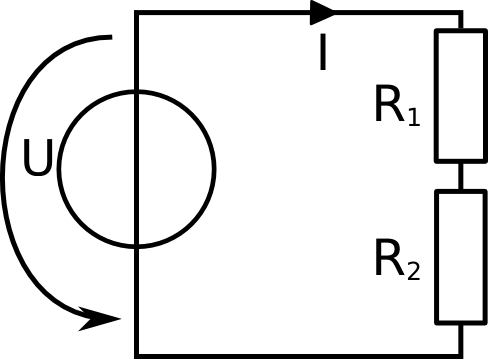
Just as in Kirchhoff's voltage law, there is also a balance for power. All power that is generated in a circuit, has to be consumed at another place. So the power that is produced by the voltage source has to be consumed by the t he only load in the circuit. If we have more than one load in a system, as in the picture below, then the total power that is produced by the votlage source needs to be consumed by the to loads. So it has to be balanced.

Ptot = P1 + P2
Ptot - P1 - P2 = 0

These two lines above both means thesame thing, you can use whichever equation you like better, they are equivalent.

How much power does the load R1 need?
U = 9 V
I = 4.5 A
R2 = 1.5 Ω

Let's have a look at a more difficult example. We need to know the power of the resistor R1. We know that the voltage source gives 9 volt and that the current in the line is 4.5 ampere. We have also found out, that the other resistor, R2 is 1.5 Ω.
To find out the power of R1, there are many different ways, I will present two different ways to find the solution. Both ways are absolutely equivalent. It does not matter which one you will take in the future, use whatever you understand the best. The first way is very long and extensive. Use thisone, when you don't feel very sure about what to do, yet. The second solution is more like a short cut. If you have done the calculations many times, then you will know exactly what to do and don't need to go through the long process.

Long solution 1:

  • for PR1 we need UR1

    To calculate the power of the resistor R1, the formula says we need the current through R1 and the voltage over R1: PR1 = UR1 * I. The current through R1 is I and we know this value, it is 4.5 A. The voltage over R1 is unknown, so we need to find out what UR1 is.

  • for UR1 we need R1

    To calculate the voltage over the resistor R1, Ohm's law says we need to know the current and the resistance: UR1 = R1 * I. As mentioned, we know the current I. So we need to find out the resistance of R1.

  • for R1 we neet Rtot

    To calcualte the resistance R1, we can use the formula Rtot = R1 + R2. We know the resistance R2, but we don't know the total resistance.

  • Rtot = U/I

    The total resistance can be calculated using the voltage and the current. According to Ohm's law, the formula is: Rtot = U/I. We know I = 4.5A and U = 9V. So we can calculate the total resistance to 9V/4.5A = 2 Ω.

  • R1 = Rtot - R2

    Using the total resistance, we can calculate the resistance of R1 = 2 Ω - 1.5 Ω = 0.5 Ω.

  • UR1 = R1 * I

    Now that we know the resistance of R1, we can calculate the voltage over R1. According to Ohm's law this is UR1 = R1 * I = 0.5 Ω * 4.5 A = 2.25 V

  • PR1 = UR1 * I

    Now that we know the voltage over R1, we can finally calculate the power demand of R1. According to the power law this is: PR1 = UR1 * I = 2.25 V * 4.5 A = 10.125 W

Quick solution 1:

  • PR1 = UR1 * I
  • UR1 = R1 * I
  • ⇨ PR1 = R1 * I * I = R1 * I2

  • R1 = Rtot - R2
  • Rtot = U / I
  • ⇨ R1 = U / I - R2

  • ⇨ PR1 = (U / I - R2) * I2
  • ⇨ PR1 = (9V / 4.5A - 1.5 Ω) * (4.5A)2 = 10.125 W

Long solution 2:

  • PR1 = Ptot - PR2

    Power can be simply added up in a similar way than with the resistances. The total power is equal to the power of resistance R1 plus the resistance R2. So we can use this formula to calculate the power demand of R1: PR1 = Ptot - PR2. So we need to find out the total power generation and the power demand of resistor R2.

  • Ptot = U*I

    The total power generation in this circuit is the voltage coming from the voltage source times the current in the circuit: Ptot = U*I = 9 V * 4.5 A = 40.5 W

  • PR2 = UR2 * I

    The power over resistor R2 is the voltage over R2 times the current through it. We know the current, it is I = 4.5 A, but we don't know the voltage UR2.

  • UR2 = R2 * I

    The voltage over R2 is calcualted using Ohm's law: UR2 = R2 * I = 1.5 Ω * 4.5 A = 6.75 V

  • PR2 = UR2 * I

    Now, we know both the current and the voltage so the equatin is: PR2 = UR2 * I = 6.75V * 4.5A = 30.375 W

  • PR1 = Ptot - PR2

    We now know both the total power and the power over R2 so we can calculate the power demand of R1: PR1 = Ptot - PR2 = 40.5 W - 30.375 W = 10.125 W

Quick solution 2:

  • PR1 = Ptot - PR2
  • Ptot = U*I
  • ⇨ PR1 = U*I - PR2

  • PR2 = UR2 * I
  • UR2 = R2 * I
  • ⇨ PR2 = R2 * I * I = R2 * I2

  • ⇨ PR1 = U*I - R2 * I2
  • ⇨ PR1 = 9 V *4.5 A - 1.5 Ω * (4.5A)2 = 10.125 W

You have now learned about electric power. You are almost finished with this course. Be sure that you still know all of the older topics as well. You are expected to be able to calculate all types of circuits and use all the rules and laws together.

Conclusion and short repetition

Let's briefly list all the important information of this chapter in a short list.

  • Electric Power is voltage times current
  • The unit of electric power is Watt [W]
  • All generated power has to be consumed again
  • P = U*I