Lection 7: Electric Energy
In this lecture, focus is laid on electric energy
Goal: The goal of this lecture is to be able to make simple calculations about energy in a circuit and to know the formula to do so.
In the last chapter, you have learn more about electric power. You already know, that power and energy is closely related. Energy is power times time.
The basic unit of energy is Joule. But in electric engineering, it is often more handy to use Watt hours instead of Joule. For you it is important to know, that these two are equivalent because Watt*hours=Joule. Have again a close look at the table:
Note: Electric Energy and Power |
| Name | Explanation | Symbols | Units | connection |
| Energy |
Energy is voltage times current times time |
E = U * I * t |
[Wh] = [V] * [A] * [h] |
E = P * t |
| Power |
Power is voltage times current |
P = U * I |
[W] = [V] * [A] |
P = E / t |
Basic example I
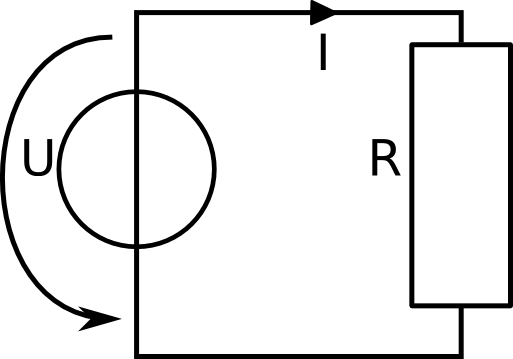
|
Simple system with the following values:
PR = 25 W
t = 1.5 h
|
|
Let's do a simple example to calculate the energy that is produced in a system.
We are given the power that is consumed by the resistance and the time the system is running.
We want to know how much energy is flowing into the resistance in this time. The formula states that energy is power times time:
| E | = | P * t | Energy is power by time |
| E | = | 25 W * 1.5 h | Using the values we are given |
| E | = | 37.5 W*h | We can use [Wh] as unit for energy... |
| E | = | 37.5 J | ...or we can use [J]. They are equivalent. |
The resistance R uses 37.5 Wh of energy during this 1.5 hours that is is connected in the network.
|
Basic example II

|
Simple system with the following values:
U = 10 V
I = 4 A
t = 210 min
|
|
In this example, we are given the voltage and current in the circuit, not the power directly.
Now, we need to know how much energy is consumed by the resistance if it runs for 210 minutes.
| E | = | P * t | Energy is power by time, but we don't know the power. |
| P | = | U * I | According to the power law, the power is voltage times current. |
| P | = | 10 V * 4 A | Using the values we are given... |
| P | = | 40 V*A | ... |
| P | = | 40 W | ... and we know the power of the resistance. |
| E | = | P * t | Now we can use the energy law: energy is power times time... |
| E | = | 40 W * 210 min | We are given the time in minutes, not in hours, so we have to transform this first. |
| [h] | = | [min]/60 | To calculate how many hours we have, divide by 60 |
| 3.5 h | = | 210min/60 | The system is running for 3.5 hours. |
| E | = | 40 W * 3.5 h | Using the values we have calculated ... |
| E | = | 150 W*h = 150 J | Using the values we have calculated ... |
The resistance R uses 150 Wh of energy during these 210 minutes that is is connected in the network.
|
Basic example III
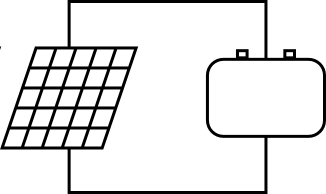
|
A solar panel is charging a battery.
On the left is the solar panel, it can deliver 120 W at 12 V output voltage.
On the right is the battery, it has a capacity of 100 Ah at an input voltage of 12 V.
|
|
This is an example as you will see it many times in solar installation. We have a 120 W solar panel with a constant output voltage of 12 V.
We want to charge a battery with an input voltage of 12 V and a maximal capacity of 100 Ah.
What is [Ah]?
When we deal with batteries, we always have to specify the output voltage.
In this case, we say that the battery gives 12 V output voltage.
The unit for energy is [Wh] which is equal to [V*A*h]. But since the voltage is known, it is very common to only specify the remaining current and time. So the unit [Ah] is used. To calculate the unit [Wh], simply multiply with the given voltage: [Ah] * [V] = [A*V*h] = [Wh]. In our example the battery has a capacity of 100 [Ah] with 12 volt output voltage so the total energy that can be stored in this battery is 100 Ah * 12 V = 1200 Wh.
Usually, when we have a circuit that runs with a battery, all devices use the same input voltage, only the current is different. For this reason, we simply omit the voltage and only deal with the current. Don't worry if this seems to complicated now, you will get used to it and see the advantage of it soon enough.
|
Back to the example, we need to know how long we need to charge the battery until it is fully charged. So we are looking for the time t.
| E | = | P * t | Energy is power by time, but we need to solve for the time. |
| t | = | E / P | Time is energy over power. |
| E | = | U * I * t = [V] * [A] * [h] = [V] * [Ah] | The energy is given by the battery specification. We know that the battery has a capacity of 100 Ah at 12 V output voltage. |
| E | = | 100 Ah * 12 V = 1200 Wh | To obtain the total energy the battery can store, multiply the two values |
| P | = | 120 W | We know the output pwer of the panel. |
| t | = | E / P | To calculate the time we need to charge the battery, we divide the total energy by the power of the panel. |
| t | = | 1200 Wh / 120 W | Using the values we are given ... |
| t | = | 10 Wh/W | Be careful with the units and try to understand how they work. |
| t | = | 10 h | And we have out result. |
The panel has to be connected to the battery for 10 hours until the battery is fully charged.
Basic example IV
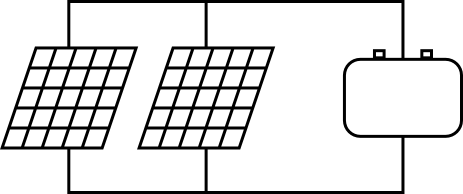
|
Two solar panels are charging a battery.
Both solar panels can deliver 200 W at 12 V output voltage.
On the right is the battery, it has a capacity of 100 Ah at an input voltage of 12 V.
|
|
In this example, there are two panels connected to the same battery. Again, we want to know how fast the battery is charged. The panels both have the same output voltage and they are connected in parallel. This is very important. In chapter 3 and chapter four, you learned about current and voltage sources. You learned, that voltage sources should only be connected in serial and current sources only be connected in parallel. Now from this constellation, what do you think a solar panel is, a voltage source or a current source?
|
In this example, we again need to calculate how much time is needed to charge the battery. But now we have two panels. So how do we work with these two panels? We have found out that panels behave like current sources. We have connected the panels in parallel. So let's have a look at this example. Both panels are 200 W and have a constant power of 12 V. We need to know how much power they have in total. Using Kirchhoff's current law, we can calculate how much current is coming out of the two panels.
| I | = | P / U = 200 W / 12 V = 16.67 A | Using the power law to calculate the current of each panel. |
| Itot | = | I1 + I2 = 16.67 A + 16.67 A = 33.33 A | The total current that is coming out of both panels and flowing to the battery can be added up, according to Kirchhoff's current law. |
| P | = | U * Itot = 12V * 33.33 A = 400 W | Using the power law to calculate the total power of both panels. To total power is just the added up power of both panels. |
| E | = | U * I * t = [V] * [A] * [h] = [V] * [Ah] | The energy is given by the battery specification. We know that the battery has a capacity of 100 Ah at 12 V output voltage. |
| E | = | 100 Ah * 12 V = 1200 Wh | To obtain the total energy the battery can store, multiply the two values |
| t | = | E / P | To calculate the time we need to charge the battery, we divide the total energy by the power of the panels. |
| t | = | 1200 Wh / 400 W | Using the values we are given ... |
| t | = | 3 Wh/W | Be careful with the units and try to understand how they work. |
| t | = | 3 h | And we have out result. |
So we have calculated, that we need to connect these two panels for 3 hours to the battery until the battery is fully charged. You see that you can connect multiple panels in parallel to get higher total power and thus charge the battery faster. This is very important. Go ask one of you teachers how many panels we have on the roof of our school. What is the total power?
Conclusion and short repetition
Let's briefly list all the important information of this chapter in a short list.
- Electric Energy is power times time
- The unit of electric energy is Watt hours [Wh] or Joule [J]
- When calculating with batteries, we often use the unit Ampere hours [Ah] at a fixed voltage input.
- All electric Energy that is generated in a system has to be consumed again.
- Solar panels can be connected in parallel to increase the total power.
|







