|
Theory |  |
Exercises |  |
 |
Lection 5.1: Kilo, Mega and Giga and SI
In this lecture, a briefe introduction into the mathematical terms of kilo, Mega and Giga is given.
Goal:The goal of this lecture is to understand the metrix unit prefixes like kilo or Mega and be able to use them. Furthermore, the SI units which replace the metric unit prefixes should be understood as well.
If you had all this already in school, then you might nit need to read through all of this text. This explanation is meant for people how do not know the prefix notation ond the SI units. If you already know them, you can have a quick look at the tables and then continue directly with the quiz and the next chapter. But be warned, from now on, the knowledge about prefixes and SI units is required. They will both be used and you should be able to handle them and understand their meaning!
If we are working woth large numbers, it is always handy to have a method to shorten these large numbers. For example if I neet to write 1'000'000 Volt, I can instead write 1 million Volts. This works, because we know that one million is equal to 1'000'000. But if we use numbers like this in calculations, it is not handy to write 3.4 million V. Instead we need another abbrevation for the word million. This abbrevation is short M. So we write only 3.4 MV instead of 3.4 million V.
These abbrevations are called metric unit prefixes. Metric unit because the units we use here are the metric system. An other system is the imperial system that is mainly used in the UK and USA. There they use ounces, pounds and stone for weight units. For distance units they use feet, yard and miles. For volume units they use ounces, pints and gallon. Some of these units are sometimes used here as well. For example miles. But in scientific use, the metric system is more commonly used.
| unit class | metric unit | imperial units UK | convertion |
|---|---|---|---|
| weight | gramm [g] | ounces [oz] pounds [lb] stone [st] |
1 ounce = 28.34952g 1 pound = 453.5923g 1 stone = 6350.2934g |
| distance | meter [m] | inches [in] feet [ft] yard [yd] mile [mi] |
1 inch = 0.0254m 1 foot = 0.3048m 1 yard = 0.9144m 1 mile = 1609.344m |
| volume | liter [l] | ounces [oz] pint [pt] gallon [gal] |
1 ounce = 0.02841306l 1 pint = 0.5682612l 1 gallon = 4.546090l |
| Note: here the UK units are used. The imperial units in the USA are slightly different from the imperial units in the UK. | |||
The idea of the metric system is that only one unit per class remains. there is no longer the need to convert from inches to feet, from feet to yards and from yards to miles. Instead, there is just one unit that deals with distances, the meter. But the be able to display this unit better, especially if we are dealing with very large, or very small numbers, the metric unit prefixes are introduced. These are prefixes that make the unit larger or smaller. For example a kilometer is the prefix kilo to the unit meter. Kilo means thousand, so a kilometer is a thousand meter. We have made a larger unit using the prefix.
Here is a table with all the prefixes that are commonly used, toghether with an example.
| name | symbol | factor | SI unit | example | |
|---|---|---|---|---|---|
| Tera | [T] | 1'000'000'000'000 | 1012 | 2.0 TB = | 2'000'000'000'000 Byte |
| Giga | [G] | 1'000'000'000 | 109 | 5.2 GW = | 5'200'000'000 W |
| Mega | [M] | 1'000'000 | 106 | 6.4 MJ = | 6'400'000 J |
| Kilo | [k] | 1'000 | 103 | 7.5 kg = | 7'500 g |
| Hecto | [h] | 100 | 102 | 5.4 hl = | 540 l |
| deci | [d] | 0.1 | 10-1 | 2.5 dl = | 0.25 l |
| centi | [c] | 0.01 | 10-2 | 36 cm = | 0.36 m |
| milli | [m] | 0.001 | 10-6 | 35 mA = | 0.035 A |
| micro | [µ] | 0.000001 | 10-6 | 600 µF = | 0.0006 F |
| nano | [η] | 0.000000001 | 10-9 | 48 ηT = | 0.000000048 T |
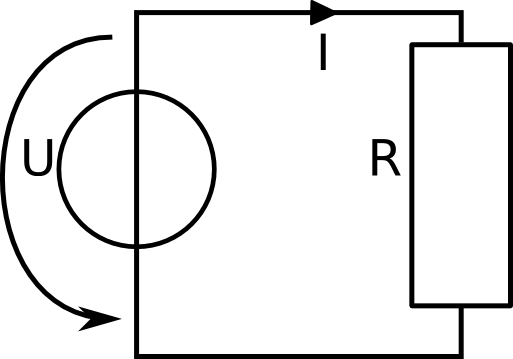
Let's have a detailed look at an example of how to use these prefixes. Assume we are to calculate the current in a small circuit as given in the picture below.
|
We know the voltage and the resistance. The formula to calculate the current is given by the first form of Ohm's law: current is voltage over resistance. In the first example, we are given the values U= 1V and R = 100 Ω. So we can calculate the current to be U/R = 1V/100Ω = 0.01 A. Now we don't like this number as it is now. We do not feel comfortable with a small number such as this. Instead, we decide to express this current not in Ampere but in milli Ampere. From the table above, we know that one milli Ampere is 0.001 Ampere. We see that 0.01 is ten times as much, so this means that 0.01 A = 10 milli Ampere or to write it in short notation 10 mA. Let's have a look at the second example. We are given the values for U = 100 V and for R = 0.1 Ω. We use again the same formula and calculate the current I = 100 V / 0.1 Ω = 1000 A. Again, we are not happy with this number. There are too many zeros. So instead of writing 1000 A we can use one of the prefixes that fits our needs. 1000 A = 10 hA = 1 kA = 0.001 MA = 0.000001 GA. From this selection, we like the kilo Ampere the best, so we write the solution simply as 1 kA. |
In the table above, there is one coloumn with the SI units. SI units are another different way to write numbers. With SI units, we can avoid prefixes and still reduce the length of the number. So how to SI units work? If you have a very large number, for example 12'000'000 V, then you can use the prefixes to write this number in a more handy form as 12 MV. But if you do not want to use the prefixes, then you can use the SI units instead. 12'000'000 V would be 12*106V. We say this is twelve times ten to the power of 6 Volts. The small number on top of the ten indicates how many zeros the ten should have. So 106 should have six zeros. 106 = 1'000'000. Look at the table below to see some examples of how to change the number to the SI units:
| normal | SI unit | factor | reformulated |
|---|---|---|---|
| 240 | 102 | 100 | 2.4 * 102 |
| 3'400 | 103 | 1'000 | 3.4 * 103 |
| 64'000'000 | 106 | 1'000'000 | 64 * 106 |
| 9'400'000'000 | 109 | 1'000'000'000 | 9.4 * 109 |
| 46'000'000'000'000 | 1012 | 1'000'000'000'000 | 46 * 1012 |
The SI units you can see in this table are only for large numbers. But before in the large table with the prefixes, there were also SI units for the very small numbers.
These work a bit differently. Take for example 0.002 A, this can be rewritten using a SI unit as 2 * 10-3 A. You see that the number on top of the ten has a minus before. That is because now we are replacing the zeros after the decimal point. With the number 0.002, we move the decimal point three positions to the right so it looks like 0002.0 and add 10-3, So we can say that the number on top of the ten moves the decimal point to the left, if the number is positive and it moves it to the right if the number is negative.
So have a look at the table below and the example given in it. Try to understand the how the SI units work and then continue on with the quiz.
| normal | SI unit | factor | reformulated |
|---|---|---|---|
| 0.33 | 10-1 | 0.1 | 3.3 * 10-1 |
| 0.015 | 10-2 | 0.01 | 1.5 * 10-2 |
| 0.015 | 10-3 | 0.001 | 15 * 10-3 |
| 0.000025 | 10-6 | 0.000001 | 25 * 10-6 |
| 0.0000005 | 10-9 | 0.000000001 | 500 * 10-9 |
If you have trouble understanding the SI units try this instruction:
| instruction | example 1 | example 2 | mathematical explanation |
|---|---|---|---|
| Write down the number you would like to transform | 12'000.0 | 0.0000024 | - |
| Move the decimal point to the left or to the right until the number looks like you want it | 12'000.0 ⇨ 12.0 | 0.0000024 ⇨ 2.4 | You are factoring out a multiple of ten. This can also be done by dividing your number by one of the factors given in the above table of SI units. By dividing your number and then multiplying the same factor again as an SI unit, you merely change the display of the number, not the value itselve. |
| write the number of position you have moved the decimal point to the left or right atop the 10. If you moved to the right, then you add a minus sign. | moved the decimal point three places to the left so I write a three on top of the ten 103 |
moved the decimal point six places to the right, so I write a minus six on top of the ten 10-6 |
The number of decimal positions you have moved your number decides which factor you have taken out of your number. This very factor then has to be replaced by the corresponding SI unit. |
| set together the two number you're finished |
12'000.0 = 12 * 103 |
0.0000024 = 2.4 * 10-6 |
Only when the new number as well as the new factor are set toghether will the number be equal to the inital value. |
Using the prefixes and the SI units needs a little bit of experience. So be sure to have a look at the exerises on the moodle.