Lecture 3.1 Resistors Part 2
In this lecture, more complicated resistors are calculated.
Goal: The goal of this lecture is to be able to calculate even difficult resistors.
In the last lecture, simple resistors in series and in parallel were calculated. Now in reality, we do not only have these simple resistors. But sometimes we have many different resistors all linked together.
It is important that you are able to still calculate the total resistance of such resistors.
|
|
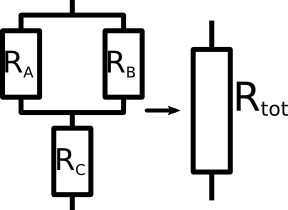
Three resistors which are both in series and in parallel. How are these calculated?
|
|
In the picture on the left is an example of a more complicated formation of resistors. How should you calculate the replacement resistor Rtot?
The trick is that you only calculate smaller parts of this network and then set them toghether. We do not know how to add up all three resistors RA, RB and RC.
But we know how to add together the two resistors RA and RB. These two resistors are in parallel. You should know the formula to add these two together.
The replacement resistor of RA and RB will be named RAB. So the formula is:
We can reformulate this to the equation below and use a calculator to give us the result.
|
|
|
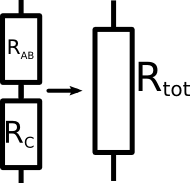
After eliminating the parallel resistors, we are left with two resistors in series.
|
|
Now the problem is simple. Only two resistors in series remain. We can just add up their resistances to get our replacement resistor Rtot.
Rtot = RAB + RC
|
You have seen now an example of how to calculate even complicated combinations of resistors. The important thing to remember is, that you only ever add up small parts and replace them with what you have calculated. Like this you will slowly but surely calculate the whole formation.
Now try ot for yourself in the next quiz.
|






