|
Theory |  |
Exercises |  |
 |
Lection 4: Ohm's Law
In this lecture, a complete DC electric circuit is treated and Ohm's law is used to calculate things.
Goal: The goal of this lecture is to set toghether the information gained in the past three lectures and have a look at a complete electric circuit. The relation between voltage, current and resistnce is explained and by the end of the lecture one should be able to calculate it. Ohm's law is introduced.
|
So far, you have seen voltage sources, current and resistors. But these three elements were always treated individually. Ohm's law is the rule to connect these three elements.The formula is: U = R * I The U stands for the voltage. The R for the resistance and I for the current. This formula means that the voltage is always equal to the current times the resistance. Of course this formula can be reformulated:
|
|||||||||||||||||||||||||||||||||||||||||||||
|
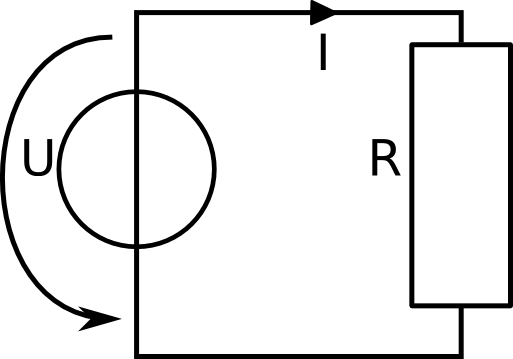
On the left is the picture of a simple electric circuit. One voltage source U, the current I and a resistor R. We re given the value of the voltage source and the resistance of the resistor:
U = 5 V we need to know the current, that is flowing through this wire. For this we use Ohm's law and Kirchhoff's voltage law. By Kirchhoff's voltage law, we know that the voltage over the resistor is the same as over the voltage source. If this is not clear to you, please revisit the chapter about voltage and do the exercises again. |
||||||||||||||||||||||||||||||||||||||||||||
|
By Ohm's law we know that the voltage over an object equals the resistance of this objecte times the current flowing through it. So in the example above we see that the voltage over the resistor R has to be the current times the resistance. Using the values we are given this leads to: 5 V = 2 Ohm * I This can be reformulated so that we can calculate the current:
Ohm's law is very important as it allowes to calculate not only simple networks as this, but even the most complex ones. Sometimes it is not strait away clear how to apply Ohm's law. Remember there are three different forms of Ohm's law. They can all be applied. And remember also Kirchhoff's law. These rules will be your most important tool with electric circuit. |
|||||||||||||||||||||||||||||||||||||||||||||
|
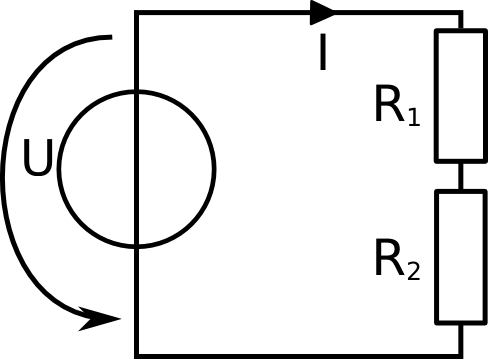
In the circuit to the left, there is one voltage source and two resistors. In this example we will calculate different values.
Example 1Given:
U = 16 V AnswerTo calculate the resistance of R2, we need to use Ohm's law and the Kirchhoff's voltage law. Apply Kirchhoff's voltage law and write down the equation for the loop you can see:
U - UR1 - UR2 = 0
The voltage from the voltage source is added as it is counter clockwise. The voltage of the loads is subtracted as it is clockwise.
UR1 = R1 * I
You see, here the second form of Ohm's law is applied. Like this we can calculate the voltage over the resistance R1. We insert the values we are given:
UR1 = 5 Ohm * 2 A = 10 V
We know now that the voltage of the resistor R1 is 10 V. Now we can use this in the Kirchhoff's voltage law from above.
U - UR1 - UR2 = 0 We have calcualted the voltage over resistor R2. The next step is to calculate the resistnace of R2. For thism we again use the Ohm's voltage law. Have a look at the note above. You can see that the last form of Ohm's law says that resistance is voltage over current. So to calculate the resitance of R2, we need to know the current flowing through the resistor and we need to know the voltage over the resistor.
R2 = UR2 / I
The solution to this problem was quite long. The important thing is to know what you need, and then find a way to the solution. Often this requires more than just one step.
In the example here, we needed to know the resistance of a certain resistor. So going backwards, we see that we could calculate this resistance, if we have the current and the voltage over this resistance. But we did not have the voltage. So we found a way to calculate the resistance. With Kirchhoff's second rule, we know that if we know the voltage U and the voltage at resistor R1, then we could calculate the voltage of the other resistor. But we didn't have the voltage over R1. To obtain this voltage we again needed Ohm's law using the resistance R1 and the current I. Once we have calculated the voltage over R1 we can calcualte the voltage over R2. Then when we know this voltage we can calculate the resistance using Ohm's law. |
||||||||||||||||||||||||||||||||||||||||||||
|
You have seen now a lot abot Ohm's law. There is just one other important formula left, and then you know the whole secret of electric circtuis. The magic is to know how to apply these laws. This might need a lot of practice. Both in the exercises and also with practical work. Conclusion and short repetitonLet's briefly list all the important information from this chapter in a short list.
|
|||||||||||||||||||||||||||||||||||||||||||||