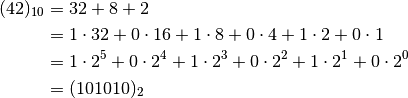16. Appendix

You really don’t know when to stop, do you?

16.1. Basic algebra

Let’s introduce some number theory. Any number can be represented by the following term:

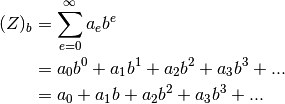
(Z)_b &= \sum_{e=0}^{\infty} a_e b^e \\ &= a_0 b^0 + a_1 b^1 + a_2 b^2 + a_3 b^3 + ... \\ &= a_0 + a_1 b + a_2 b^2 + a_3 b^3 + ...

Now, that was very abstract. Let’s explain first, then make some examples.

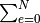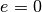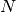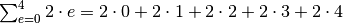The first thing you need to know is the numbers sign \sum_{e=0}^{N}. It’s just a shorthand notation for a sum of many terms. The terms can use a sum variable e which starts from an initial value e=0 and goes to some maximum value N. So \sum_{e=0}^4 2 \cdot e = 2 \cdot 0 + 2 \cdot 1 + 2 \cdot 2 + 2 \cdot 3 + 2 \cdot 4.

We also use two exponential laws, namely

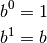
b^0 &= 1 \\ b^1 &= b

Let’s make an example with base 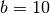b=10.

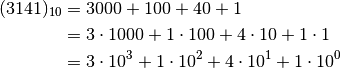
(3141)_{10} &= 3000 + 100 + 40 + 1 \\ &= 3 \cdot 1000 + 1 \cdot 100 + 4 \cdot 10 + 1 \cdot 1 \\ &= 3 \cdot 10^3 + 1 \cdot 10^2 + 4 \cdot 10^1 + 1 \cdot 10^0 \\

Let’s now write the same number in the binary system.

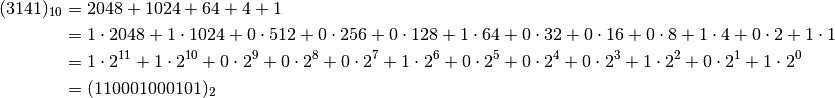
(3141)_{10} &= 2048 + 1024 + 64 + 4 + 1 \\ &= 1 \cdot 2048 + 1 \cdot 1024 + 0 \cdot 512 + 0 \cdot 256 + 0 \cdot 128 + 1 \cdot 64 + 0 \cdot 32 + 0 \cdot 16 + 0 \cdot 8 + 1 \cdot 4 + 0 \cdot 2 + 1 \cdot 1 \\ &= 1 \cdot 2^{11} + 1 \cdot 2^{10} + 0 \cdot 2^9 + 0 \cdot 2^8 + 0 \cdot 2^7 + 1 \cdot 2^6 + 0 \cdot 2^5 + 0 \cdot 2^4 + 0 \cdot 2^3 + 1 \cdot 2^2 + 0 \cdot 2^1 + 1 \cdot 2^0 \\ &= (110001000101)_2

Since we’re dealing with computers, here’s an example with base 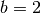b=2. Let’s write the number 42 in binary.

(42)_{10} &= 32 + 8 + 2 \\ &= 1 \cdot 32 + 0 \cdot 16 + 1 \cdot 8 + 0 \cdot 4 + 1 \cdot 2 + 0 \cdot 1 \\ &= 1 \cdot 2^5 + 0 \cdot 2^4 + 1 \cdot 2^3 + 0 \cdot 2^2 + 1 \cdot 2^1 + 0 \cdot 2^0 \\ &= (101010)_2 \\

16.2. Cryptography notes